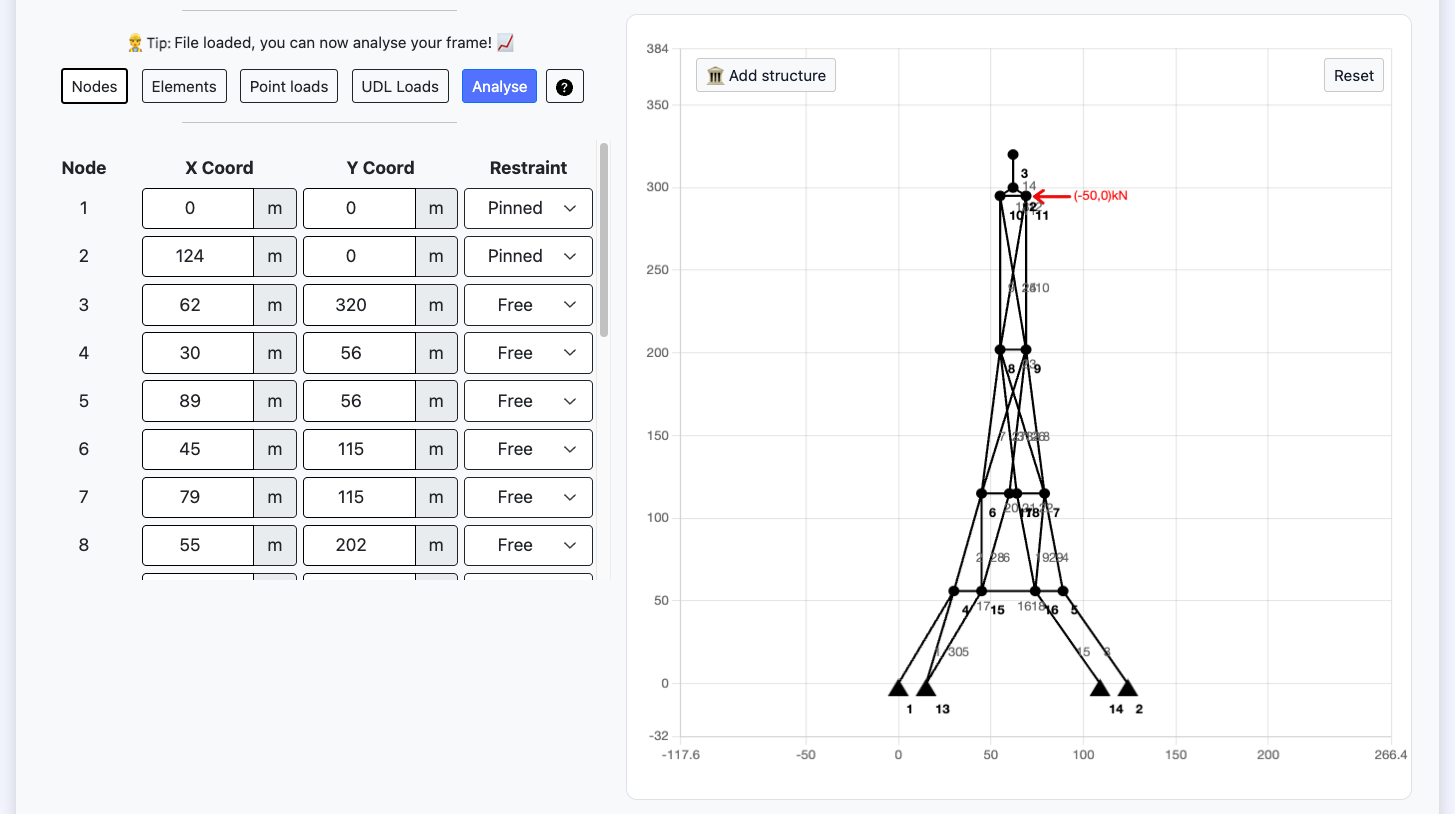
Free Slope Stability Analysis
Calculate the slope stability design factor of safety, find the critical slip surface.
Please wait, generating all slip surfaces...
Loading...
Results Summary
| Analysis Result | |
| Critical safety factor |
Slope properties
Slope height
m
Slope height cannot be greater than soil depth.
Slope length
m
Water depth
m
Water depth cannot be greater than soil depth.
Apply surcharge
What is slope analysis?
Slope stability analysis is a undertaken by a Geotechnical Engineer to understand the likelihood and risk of slope failure. Slope failure is both dynamic and static and be solved by either limit equilibrium methods, empirical methods or finite element analysis methods.
How is slope stability analysed?
Slope failure, otherwise known as a landslide or rockfall, is a phenomenon where ground in a non-equilibrium state is displaced under the action of gravity the earth is displaced until it reaches a new equilibrium condition. Slopes can fail in different ways depending on slope geology profile and if there are any fractures within the earth. However when failure occurs it is sudden typically without many warning signs. If a slope is susceptible then failure usually occurs after a period of heavy rain which results in changes to the ground water table.
What are the slope failure types?
There are a wide range of slope failure mechanisms here we cover some of the most common failure types plane failure commonly occurs when discontinuities through the slope intersect to form a planar surface along which the block is free to move which failure occurs when two discontinuities intersect whose lines of intersection are approximately perpendicular to the strike of the slope and dip towards the plane of the slope circular failure follows a similar principle to wedge failure toppling failure occurs when columns of rock form by steep discontinuities rotate about a fixed point at or near the base of the slope followed by slip between the layers rotational slips are the most common form of slope failure and follow a circular arc through the soil translational slips are also common which are typically found when the topsoil layer is underlain by a soil of very different strength.
How to calculate the factor of safety for slope stability
We can use seven calculation stages to determine a slope stability factor of safety:
- Define the 2d geometry considering things like slope height and length
- Define a failure surface which we assume the slope is failing along
- Split the model into a number of different slices the greater the number of slices the more accurate the calculation
- Calculate the weight of each size
- Calculate the resisting force on each slice
- Calculate the destabilising force on each slice
- Calculate the factor of safety between resistance and destabilising forces
We repeat this process for all possible failure surfaces.
After defining the 2d geometry and water table level, we assume a circular failure surface through the slope. For now we can define the center of this failure slope and radius at an arbitrary location, we then divide the slope within the bounds of the failure surface into a number of slices (the more the better). After we have split the slope into a number of slices we can consider these slices individually, each slice follows the slope at an angle, each slice has a weight, normal force and water pressure. There is also shear resistance acting on the slope base and vertical shear resistance between each slice. The weight of each slice is calculated using the density and area of the slice.
Calculate the resisting forces on each slice: The calculation uses the Moore-Coulomb failure criterion to calculate the shear resistance of each slice. This equation uses the cohesion, normal force and friction angle. Calculate normal effective force for each slice using the weight, slice angle, pore water pressure and arc length of the slice base. The corresponding friction force is calculated using the effective normal stress and the friction angle. The cohesive resistance force is calculated using the cohesion and slice length. The overall resistance is calculated as the sum of the friction and cohesion resistance
Calculate the destabilising forces on each slice: These forces are calculated using the weight of each slice and the angle of the slice base from horizontal
The factor of safety of the slope is calculated: The calculation uses the ratio between the sum of the resisting and sum of the destabilising forces acting on all slices.
Calculation stages one to seven should then be repeated for all possible failure surfaces of the slope with the worst case factor of safety than adopted.
What is the limit equilibrium method for slope stability and the Bishop’s method?
Soil slopes can be analysed in a number of different ways, using methods such as the limit equilibrium approach or finite element analysis. This explanation will focus on the limit state approach. This method identifies potential failure mechanisms and derives factors of safety for a particular geotechnical situation. Many different solution techniques for the limit state equilibrium method of slices have been developed over the years and all are similar for solving soil and rock slope analysis. The differences between the methods depend on: what equations of statics are included and satisfied and which interslice forces are included and what is the assumed relationship between the interslice shear and normal forces. In later years slope stabilisation and the beneficial effect of ground anchors and soil nails have been considered in calculating the slope stability factor of safety.
Limit equilibrium types of analyses for assessing the stability of earth slopes have been in use in geotechnical engineering for many decades. The idea of discretizing a potential sliding mass into vertical slices was introduced early in the 20th century and is consequently the oldest numerical analysis technique in geotechnical engineering.
Bishop (1955) devised a scheme that included interslice normal forces, but ignored the interslice shear forces. Again, Bishop’s Simplified method satisfies only moment equilibrium. Of interest and significance with this method is the fact that by including the normal interslice forces, the factor of safety equation became nonlinear and an iterative procedure was required to calculate the factor of safety
In the 1950’s Professor Bishop at Imperial College in London devised a method which included interslice normal forces, but ignored the interslice shear forces. Bishop developed an equation for the normal at the slice base by summing slice forces in the vertical direction. The consequence of this is that the base normal becomes a function of the factor of safety. This in turn makes the factor of safety equation nonlinear (that is, FS appears on both sides of the equation) and an iterative procedure is consequently required to compute the factor of safety.
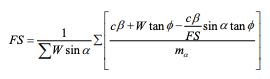
FS is on both sides of the equation as noted above. The equation is not unlike the Ordinary factor of safety equation except for the m term, which is defined as:
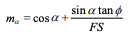
Note that in this case the moment factor of safety (Fm) is insensitive to the interslice forces. The reason for this, as discussed in the previous chapter, is that no slippage is required between the slices for the sliding mass to rotate. This is not true for force equilibrium and thus the force factor of safety (Ff) is sensitive to the interslice shear. In summary, the Bishop’s Simplified method, (1) considers normal interslice forces, but ignores interslice shear forces, and (2) satisfies over all moment equilibrium, but not overall horizontal force equilibrium.
Calculation validation

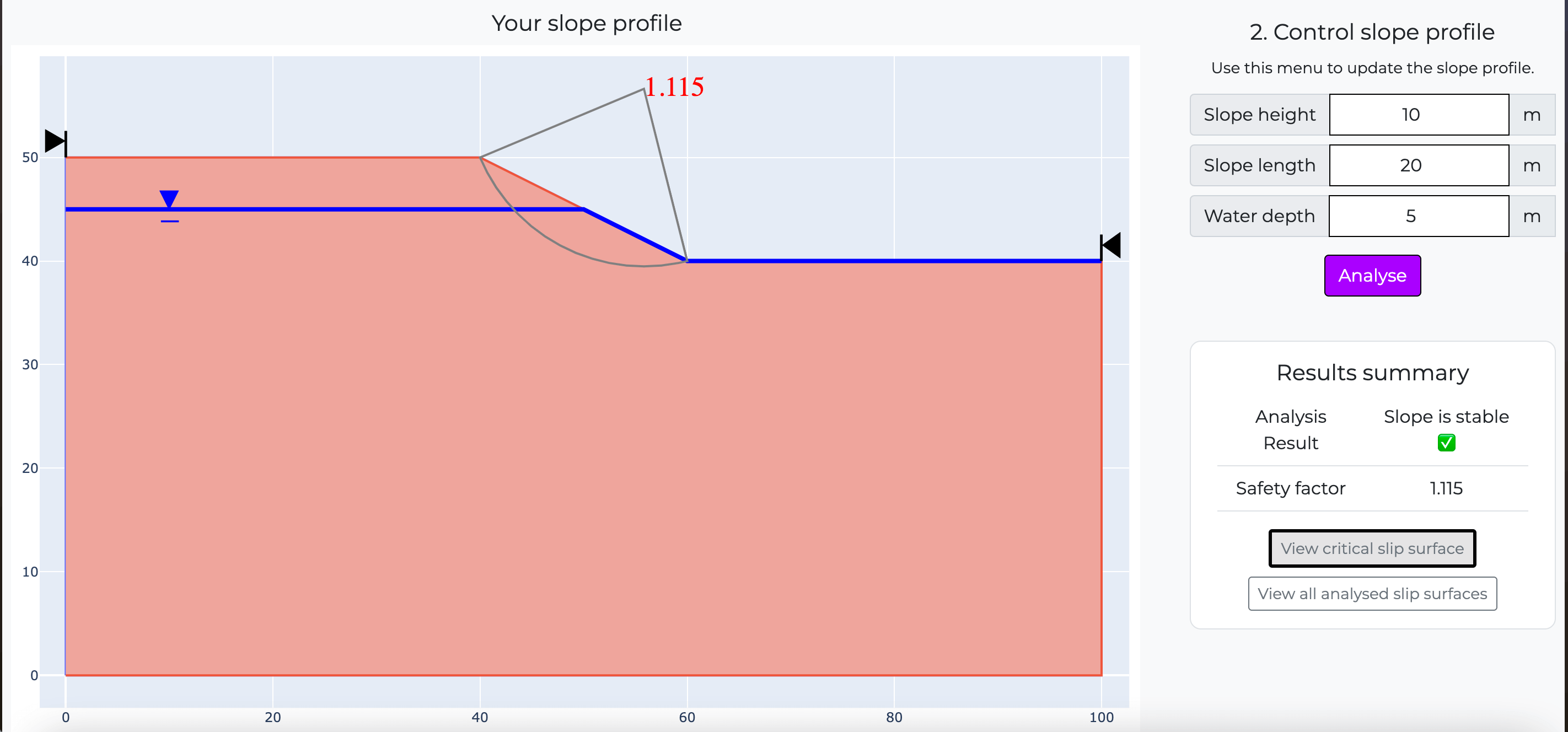
What's this calculator used for?
This free slope stability analysis calculator can be used by Geotechnical Engineers to calculate the factor of safety of a slopes slip surfaces. Using this calculator slopes can be analysed with the limit equilibrium Bishop's method of slices to calculate the factor of safety and overall stability of a slope. With this calculator slopes can be designed for surcharge and point loads to calculate factor of safety. This calculation uses 50 slices and 2500 iterations. Water table level through the slope and multiple soil layers are considered.
Contribute to this open-source calculator
This calculator is open-source and you can contribute to it's development.
You can find the source code on GitHub here: PySlope
Special credits: Jesse Bonanno
Interested in learning more about automation?

Enroll on our training certifications and learn how to code, build AI applications with no-code tools and automate tasks.
UDL Control Panel
| Magnitude | Offset from crest | Load length | |
|---|---|---|---|
|
kN/m
|
m
|
m
|
Point Load Control Panel
| Magnitude | Offset from crest | |
|---|---|---|
|
kN
|
m
|